Notebooks
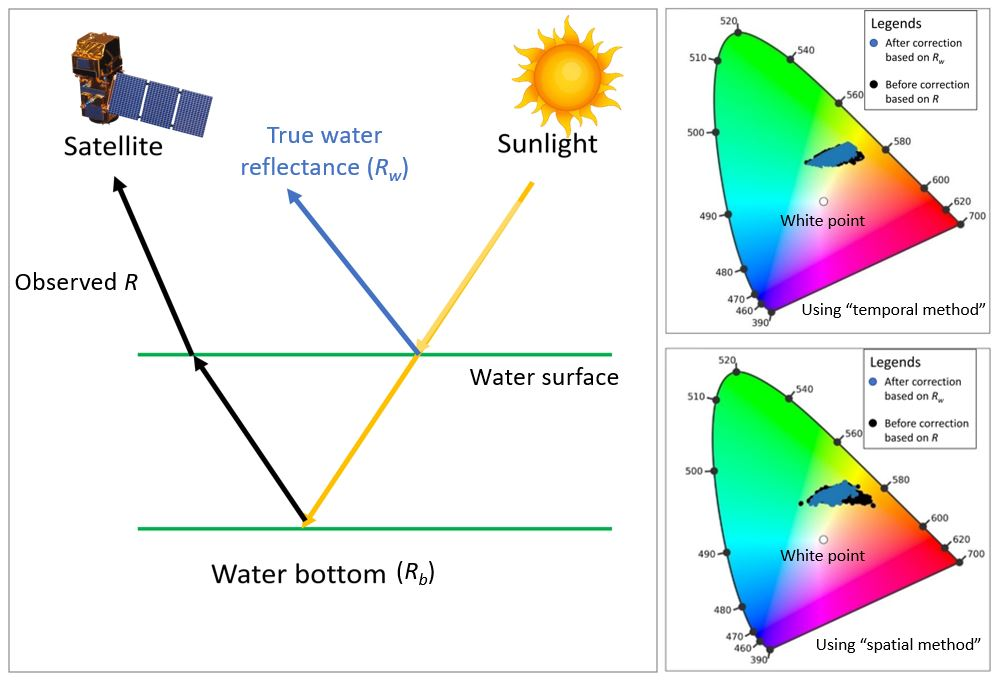
Removing the contribution of seabed reflectance to water reflectance
Description:
<!--StartFragment--> ## **To anyone who would like to use my model to correct water reflectance in the intertidal regions:** Lyzenga's model is widely used to estimate water depth or water reflectance at infinite depths. Rewrite the Lyzenga's model into Equation 1: 𝐾𝑑(𝑖)(𝜆)=1/(2𝑧𝑖)×ln(𝑅𝑏(𝜆)−𝑅𝑤,(𝜆)𝑅𝑖(𝜆)−𝑅𝑤(𝜆)) #(1) There are two unknown parameters Rw and Kd. *In order to estimate Rw and Kd, we assume Kd does not change against water depth over a short scale. Because water depth can vary due to tides or elevation of the loction. Therefore, we have two methods to do the correction (for more detials please check the paper: [https://doi.org/10.3390/rs15010011](https://colab.research.google.com/corgiredirector?site=https%3A%2F%2Fdoi.org%2F10.3390%2Frs15010011)). Here I demonstrate one of them (Spatial Method). The used data is from Sentinel-2 L2A scanned in Tauranga Harbour.* *Have a look at the complete codes:* https://colab.research.google.com/drive/11CeKUxdM_yzrNU61qVnIRVNRZiaUsOEt?usp=sharing - - - <!--EndFragment-->
Metadata:
Ocean
Zhanchao Shao, Karin Bryan, Moritz Lehmann, Conrad Pilditch (zs94@students.waikato.ac.nz)
Non-standard
Python
Datasets:
Content:
## Show the relationship import cv2 import numpy as np #reflectance_B2 = cv2.imread('filepath',-1) #water_depth = cv2.imread('filepath',-1) ###Make sure water depth is accurate or it will substaintially change the result... reflectance_B2 = np.array([0.0815, 0.0693, 0.0583, 0.0729, 0.0619, 0.0523, 0.0647, 0.0614, 0.0592]) water_depth = np.array([0.2, 0.305, 0.417, 0.289, 0.391, 0.544, 0.345, 0.558, 0.630])-0.19 import matplotlib.pyplot as plt plt.scatter(water_depth,reflectance_B2) plt.xlabel('water depth (m)') plt.ylabel('Reflectance B2') ###RANSAC will be a good tool to remove the outliers which reduce the uniformity from sklearn.linear_model import RANSACRegressor # Apply RANSAC import random random.seed(10) ransac = RANSACRegressor(max_trials=5) # The values for the hyperparameters might be different too. ransac.fit(water_depth.reshape(-1,1), reflectance_B2) # Predict using all data line_X = np.arange(0.1, 0.7, 0.01).reshape(-1, 1) # Range for water_depth line_y_ransac = ransac.predict(line_X) # Identify inliers and outliers inlier_mask = ransac.inlier_mask_ outlier_mask = np.logical_not(inlier_mask) # Plot plt.scatter(water_depth[inlier_mask], reflectance_B2[inlier_mask], color='blue', label='Inliers') plt.scatter(water_depth[outlier_mask], reflectance_B2[outlier_mask], color='red', label='Outliers') plt.xlabel('Water Depth') plt.ylabel('Reflectance B2') plt.legend() plt.show() wd = water_depth[inlier_mask][1:] R = reflectance_B2[inlier_mask][1:] Rw =np.arange(0.01,np.nanmin(R),np.nanmin(R)/100) Error2 = [] Error = [] for i in range(len(Rw)): ###We start to guess. Rw should range from 0 to R. And the correct Rw should make sure the relationship between kd and wd is flat. Ideally the variances between Rw and Kd is also minimum a = np.polyfit(wd,np.log((0.0889-Rw[i])/(R-Rw[i]))/(2*wd),1) #Rb can be derived when emerged Error2.append(a[0]) variance = np.nanstd(np.log((0.0889-Rw[i])/(R-Rw[i]))/(2*wd))#We can actually guess the appropriate value of Rb Error.append(variance) Error2 = np.array(Error2) Error = np.array(Error) plt.plot(Rw,abs(Error2)) plt.xlabel('Rw') plt.ylabel('S') plt.show() plt.plot(Rw,Error) plt.xlabel('Rw') plt.ylabel('Variance') plt.show() absErr = np.abs(np.array(Error)) ##Find out the Rw value when Variance is minimized. absErr = absErr.tolist() min_index = absErr.index(min(absErr)) rw = Rw[min_index] rw
